问题
解答题
设函数f(x)＝a2ln x－x2＋ax，a>0.
①求f(x)的单调区间；②求所有实数a，使e－1≤f(x)≤e2对x∈[1，e]恒成立．
答案
①f(x)的增区间为(0，a)，减区间为(a，＋∞)．②a＝e
①f(x)＝a2ln x－x2＋ax，其中x>0，
所以f′(x)＝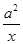
－2x＋a＝
.
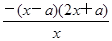由于a>0，∴由f′(x)>0知0<x<a，
由f′(x)<0知x>a.
所以，f(x)的增区间为(0，a)，减区间为(a，＋∞)．
②由题意知f(1)＝a－1≥e－1，
即a≥e.
由①知f(x)在[1，e]内递增，
要使e－1≤f(x)≤e2对x∈[1，e]恒成立．
只要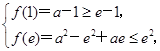
∴a＝e.