阅读下面的文字,完成文后各题。
巴尔塔萨的一个奇特的下午
【哥伦比亚】加卡列尔•加西亚•马尔克斯
鸟笼做成了。巴尔塔萨习惯地把它挂在房檐底下。刚吃完午饭,就听人到处在说,他做了一个全世界最漂亮的鸟笼。来瞧热闹的人多级了,巴尔塔萨房前简直门庭若市,吵吵嚷嚷的,他只得摘下鸟笼,把木工作坊的门关上。
“你该刮刮脸啦。”乌尔苏拉对他说。两个星期以来,丈夫一心扑在鸟笼上,干木工活儿就不用心思了,她很不高兴,可是鸟笼一做好,她的烦恼就顿时烟消云散了。
“你能赚多少钱呢?”她问。
“不知道,”巴尔塔萨回答,“我想要价三十比索。末了总能到手二十吧。”
“你先要五十比索,”这半个月来,你起早贪黑的。再说,这鸟笼多大呀。我这辈子见过的鸟笼,就数这个大哩。”
有关鸟笼的消息早就传开了,老大夫希拉尔多的夫人爱养鸟,那天下午,大夫出诊归来,就去看个究竟。
饭厅里挤满了人,那鸟笼放在桌上,供人观赏。偌大的鸟笼用铁丝扎成,分成三层,上下有通道,里面搭着专供鸟儿吃食和栖息的小房。空余部分,装有鸟儿嬉戏用的吊杆。整个鸟笼,犹如一座大型冰厂的模型。老大夫左看右瞧,他寻思,这鸟笼果然名不虚传,比他想给妻子买的那种漂亮多了。
“这鸟笼根本不用养鸟,只要在树上一挂,它自己就会叫起来。”说着,他当着众人把鸟笼转了几转,又把鸟笼搁回桌上,“得,我买下了。”
“已经卖给别人啦。”乌尔苏拉说。
“蒙铁尔的儿子,是他订做的。”巴尔塔萨补充道。
大夫又瞧瞧鸟笼。“你可以再做一个嘛!”
“很抱歉,大夫,”巴尔塔萨说,“可是已经出手的东西是不能再卖的呀。”
大夫耸耸肩膀,“他们出多少钱买下的?”
巴尔塔萨把目光转向乌尔苏拉。“六十个比索。”她说。
大夫又看看鸟笼。“真漂亮,”他赞叹着,“漂亮极了。”说罢,转身朝门口走去,“蒙铁尔可真有钱啊!”
财主蒙铁尔对于鸟笼的新闻无动于衷。他就住在离这儿没有多远的地方,一间堆满家具什物的房子里。他那形容憔悴的妻子,一吃罢午饭就紧闭门窗,在黑洞洞的屋子里,睁着眼睛整整待上两个钟头。她忽然听见人声嘈杂,不禁吃了一惊。开门一看,只见门前聚集着一大帮人,巴尔塔萨拿着一个鸟笼也在那儿。他穿一身白,胡子刮得精光,神情严肃纯朴。
“这玩意儿真太妙啦,”蒙铁尔的妻子喊了起来,顿时容光焕发,她把巴尔塔萨请到屋里,“我这一辈子都没见过这么好的玩意儿。”
“彼贝在家吗?”巴尔塔萨把鸟笼搁在饭厅的桌子上。
“他还在学校里呢,一会儿就回来。”她答道。接着补上一句:“蒙铁尔这会儿在洗澡呢。”
蒙铁尔体态肥大,浑身毛茸茸的,脖子上搭着一条毛巾,从卧室的窗户里探出身来:“那是什么呀?”
“彼贝的鸟笼呗。”巴尔塔萨说。
那女人疑惑地瞧他一眼:“是谁的?”
“彼贝的呀,”巴尔塔萨的语气十分肯定,“是彼贝让我做的呀。”
蒙铁尔穿着裤衩就从卧室走了出来。“彼贝!”他大喊了一声。
“孩子还没有回来呢。”他妻子喃喃地说。
彼贝在门洞里出现了。他约摸十二岁,眼睫毛弯弯的,沉静忧伤,活像他母亲。
“你过来,”蒙铁尔对他说,“是你让他们做鸟笼的吧?”
孩子低下脑袋。蒙铁尔一把揪住孩子头发,硬要孩子看着他的眼睛,“你说呀。”
孩子咬咬嘴唇,一声不吭。
“蒙铁尔!”妻子埋怨了。
蒙铁尔放开孩子,转身朝巴尔塔萨走来。“抱歉得很哪,巴尔塔萨,你事先应该跟我商量一下嘛。只有你才会跟小孩子打交道。”他把鸟笼还给巴尔塔萨,“你赶紧拿走,能卖给谁就卖给谁。”
那孩子一直木然不动地呆着,连眼皮都不眨一下。等巴尔塔萨接过鸟笼,迟疑地瞧了他一眼,他才像狗打呼噜似的,喉咙里发出一声闷响,然后趴到在地,嚎啕大哭。
蒙铁尔冷眼瞧着,无动于衷。母亲想上去抚慰一阵。“别管他。”蒙铁尔毫不妥协。
巴尔塔萨瞧那孩子半死不活的,活像一头害了传染病的牲畜。
“彼贝!”巴尔塔萨笑盈盈地走到孩子跟前,把鸟笼递给他。那孩子一跃而起,抱住跟他差不多大小的鸟笼,透过密集的铁丝瞧着巴尔塔萨,不知说什么好。
“巴尔塔萨 ,” 蒙铁尔轻声说,“我不是说了吗,你把鸟笼拿走吧。”
“还给人家吧。”母亲吩咐孩子。
“你留着吧。” 巴尔塔萨说。
“你别犯傻了,巴尔塔萨,” 蒙铁尔边说边拦住他,“你把这玩意儿带回家去吧,我一个子儿也不会给你的呀。”
“没事儿。我就是特意做了送给彼贝的,没想过要什么钱嘛。”
巴尔塔萨从挤在门口瞧热闹的人群里拨开一条路,走了出去。
巴尔塔萨在台球房受到热烈欢迎。这时候,他还在想,他做的鸟笼比别人的好,为了不让蒙铁尔的儿子哭哭啼啼,只得把鸟笼送给他,诸如此类的事情没什么新鲜的。可是过不了多久,他发现这类事情对许多人还挺重要,不禁兴奋起来。
“他们到底还是给了你五十比索才买下鸟笼的吧。”
“六十比索。”巴尔塔萨答道。众人给巴尔塔萨斟上一杯啤酒,他一一回敬。天刚擦黑,他就喝得酩酊大醉,漫无边际地胡扯起来。他说他要做一千个鸟笼,每个售价六十比索。然后,再做它一百万个,攒满六千万比索。电唱机由他出钱不停地唱了整整两个钟头。大家举杯敬祝巴尔塔萨身体健康,走运,幸福。
乌尔苏拉做好一盘葱头炸肉,一直等他。有人告诉她,她丈夫在台球房里欢喜若狂地跟大伙儿喝啤酒呢。她不相信,因为巴尔塔萨从来没有喝过酒。差不多半夜了,巴尔塔萨还在灯火通明的台球房里,一步也动弹不得。他花了不少钱,只得留下手表抵押,保证次日还清欠款。过了一会儿,他劈腿坐在街上。清晨五点钟,赶去望弥撒的妇女们看见他还坐在那儿。
(选自高兴主编《小说中的小说》,有删改)
小题1:请用简明的语言梳理这篇小说的脉络。(5分)
小题2:依据小说的相关内容,概括蒙铁尔形象的特点。(5分)
小题3:指出小说中画线处所用的描写方法,并分析这段文字在情节发展上的作用。(4分)
小题4:小说的结尾部分,写了从来没喝过酒的巴尔塔萨喝得酩酊大醉,这样安排有什么作用?根据小说,请从两个不同的角度谈谈你的见解。(6分)
 );(2)
);(2)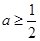 .
.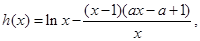 则a=0时,由(1)显然不成立;然后根据导函数的性质,求满足h(x)的最大值小于0的a的取值范围即可.(可分
则a=0时,由(1)显然不成立;然后根据导函数的性质,求满足h(x)的最大值小于0的a的取值范围即可.(可分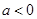 ,
,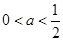 ,
,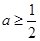 三种情况去验证.)
三种情况去验证.)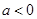 ,
,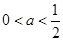 ,
,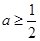 ,求
,求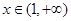 时,h(x)的最大值小于0即可,
时,h(x)的最大值小于0即可,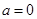 ,
,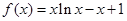 ,
,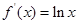
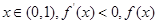 为减函数,
为减函数,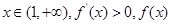 为增函数.
为增函数.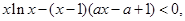 在
在 恒成立.
恒成立.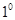 若
若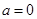 ,
,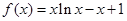 ,
,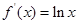
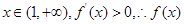 为增函数.
为增函数.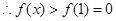
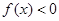 不成立;
不成立;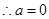 不成立.
不成立.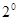
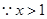 ,
, 在
在 恒成立,
恒成立,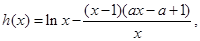
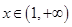
 ,
,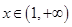
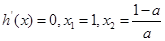 ,
,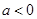 ,则
,则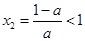 ,
,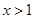 ,
, ,
,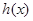 为增函数,
为增函数,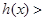
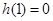 (不合题意);
(不合题意);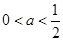 ,
,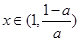 ,
, ,
,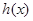 为增函数,
为增函数,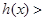
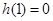 (不合题意);
(不合题意);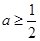 ,
,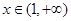 ,
,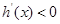 ,
,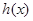 为减函数,
为减函数,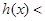
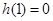 (符合题意).
(符合题意).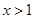 时,
时,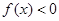 恒成立,则
恒成立,则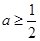 .
.