问题
填空题
Rt△ABC中，A=30°，BC=2，将Rt△ABC沿斜边AC所在直线旋转一周，那么所得几何体的体积为 ______．
答案
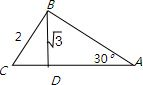
Rt△ABC中，A=30°，BC=2，将Rt△ABC沿斜边AC所在直线旋转一周，
旋转体可以看作是由两个相同底面的圆锥构成的，
底面半径为
，如图3
圆锥的体积为：
×(1 3
)3π ? CD+3
×(1 3
)2π ?AD=4π．3
故答案为：4π
搜题请搜索小程序“爱下问搜题”