问题
解答题
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
答案
(1) 函数f(x)的单调递增区间为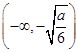 和
和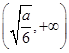 ,
,
单调递减区间为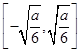 .
.
(2)见解析
(1)由题意得f′(x)=12x2-2a.
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞).
当a>0时,f′(x)=12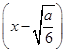
 ,
,
此时函数f(x)的单调递增区间为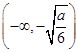 和
和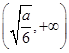 ,
,
单调递减区间为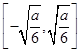 .
.
(2)证明:由于0≤x≤1,故当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2.
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2.
设g(x)=2x3-2x+1,0≤x≤1,则
g′(x)=6x2-2=6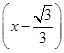
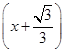 .
.
于是
| x | 0 | 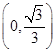 |  | 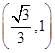 | 1 |
| g′(x) | - | 0 | + | ||
| g(x) | 1 | 减 | 极小值 | 增 | 1 |
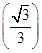 =1-
=1-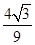 >0.
>0.所以当0≤x≤1时,2x3-2x+1>0.
故f(x)+|a-2|≥4x3-4x+2>0.
