问题
填空题
设函数y＝f(x)，x∈R的导函数为f′(x)，且f(x)＝f(－x)，f′(x)＜f(x)．则下 * * 个数：ef(2)，f(3)，e2f(－1)从小到大依次排列为________．(e为自然对数的底数)
答案
f(3)＜ef(2)＜e2f(－1)
构造函数g(x)＝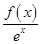
，g′(x)＝
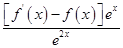＜0，所以g(x)在R上为减函数，得g(1)＞g(2)＞g(3)，即
＞
＞
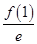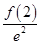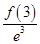，得e2f(1)＞ef(2)，e3f(2)＞e2f(3)，即ef(2)＞f(3)，又f(－1)＝f(1)，所以f(3)＜ef(2)＜e2f(－1)．