问题
解答题
设函数
(1)试问函数能否在处取得极值,请说明理由;
(2)若,当时,函数的图像有两个公共点,求的取值范围.
答案
(1)函数不能在处取得极值,理由详见试题解析;
(2)的取值范围是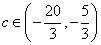 .
.
题目分析:(1)先对函数求导,因为函数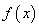 在实数
在实数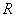 上单调递增,故函数不可再
上单调递增,故函数不可再
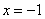 处取得极值.
处取得极值.
(2)函数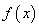 与
与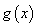 的图像在
的图像在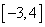 有两个公共点,即方程
有两个公共点,即方程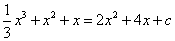 在
在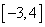 有两解,结合函数的单调性可求的取值范围.
有两解,结合函数的单调性可求的取值范围.
(1)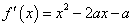 ,当
,当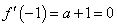 时,
时,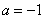 ,
,
而此时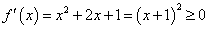 ,函数
,函数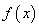 在实数
在实数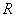 上单调递增,故函数不可再
上单调递增,故函数不可再
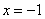 处取得极值.
处取得极值.
(2)当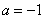 时,
时,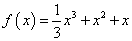 ,函数
,函数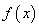 与
与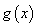 的图像在
的图像在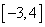 有两个公共点,即方程
有两个公共点,即方程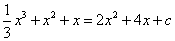 在
在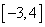 有两解,
有两解,
方程可转化为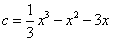 ,设
,设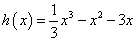 ,
,
则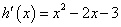 ,令
,令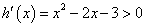 ,
,
解得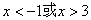 ,所以
,所以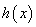 函数在
函数在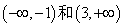 递增,在
递增,在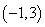 上递减.
上递减.
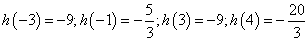 ,所以要使得方程有两解需
,所以要使得方程有两解需
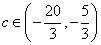 .
.
