问题
解答题
设函数f(x)=2x3-3(a-1)x2+1,其中a≥1.求函数f(x)的单调区间和极值.
答案
详见解析.
题目分析:(1)先求导数fˊ(x),求出f′(x)=0的值,然后讨论a=1与a>1两种情形,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的单调区间;(2)讨论a=1与a>1两种情形,根据(1)可知f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的极值.
由已知得f(x)=6x[x-(a-1)],令f(x)=0,解得 x1=0,x2=a-1,.
(1)当a=1时,f(x)=6x2,f(x)在(-∞,+∞)上单调递增
当a>1时,f(x)=6x[x-(a-1)],f(x),f(x)随x的变化情况如下表:
| x | (-∞,0) | 0 | (0,a-1) | a-1 | (a-1,+∞) |
| f(x) | + | 0 | 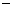 | 0 | 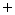 |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
从上表可知,函数f(x)在(-∞,0)上单调递增;在(0,a-1)上单调递减;在(a-1,+∞)上单调递增.
(2)由(1)知,当a=1时,函数f(x)没有极值.;当a>1时,函数f(x)在x=0处取得极大值,在x=a-1处取得极小值1-(a-1)3.
