若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知A,b是实数,1和-1是函数f(x)=x3+Ax2+b x的两个极值点.
(1)求A和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
(1) 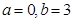 ;(2) 函数g(x)的极值点为
;(2) 函数g(x)的极值点为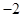 .
.
题目分析:(1)极值点时,函数取得极值,对应的导函数的值为 ,先对函数求导得
,先对函数求导得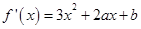 ,当
,当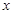 取
取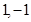 时,导函数值为
时,导函数值为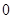 ,得到关于
,得到关于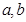 的二元一次方程,解得
的二元一次方程,解得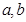 的值;(2)由
的值;(2)由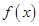 知
知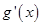 ,令
,令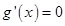 得
得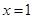 或
或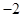 ,两数将定义域分成三个部分,根据极值定义列表判断,可知当
,两数将定义域分成三个部分,根据极值定义列表判断,可知当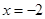 时函数有极小值.
时函数有极小值.
解:(1)因为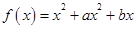 ,
,
所以f′(x)=3x2+2Ax+b,且f′(-1)=3-2A+b=0,f′(1)=3+2A+b=0,
解得A=0,b=-3. 4分
经检验,当A=0,b=-3时,1和-1是函数f(x)=x3+Ax2+bx的两个极值点.
综上,所求的A和b的值分别为0,-3. 5分
(2)由(1),知f(x)=x3-3x,所以g′(x)=x3-3x+2=(x-1)2(x+2),
令g′(x)=0,得x=1或x=-2, 7分
当x变化时,g′(x),g(x)的变化情况如下所示:
| x | (-∞,-2) | -2 | (-2,1) | 1 | (1,+∞) |
| g′(x) | - | 0 | + | 0 | + |
| g(x) | ↘ | 极小值 | ↗ | 不是极值 | ↗ |
所以x=-2是函数g(x)的极小值点,
即函数g(x)的极值点为-2. 12分
