问题
解答题
已知f（x）=x2，g（x）=x3，求适合f′（x）+1= g′（x）的x值。
答案
解：由导数的公式知，f′（x）=2x，g′（x）=3x2，
因为f′（x）+1=g′（x），
所以2x+1=3x2，
即3x2-2x-1=0，
解得x=1或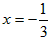
。
搜题请搜索小程序“爱下问搜题”
已知f（x）=x2，g（x）=x3，求适合f′（x）+1= g′（x）的x值。
解：由导数的公式知，f′（x）=2x，g′（x）=3x2，
因为f′（x）+1=g′（x），
所以2x+1=3x2，
即3x2-2x-1=0，
解得x=1或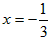。