问题
解答题
已知函数f(x)＝x3－ax2－3x.
(1)若f(x)在[1，＋∞)上是增函数，求实数a的取值范围；
(2)若x＝3是f(x)的极值点，求f(x)的单调区间．
答案
（1）a≤0
（2）f(x)的单调递增区间为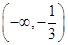
，[3，＋∞)，f(x)的单调递减区间为
.
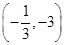解：(1)对f(x)求导，
得f′(x)＝3x2－2ax－3.
由f′(x)≥0，得a≤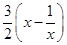
.
记t(x)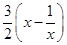＝，当x≥1时，t(x)是增函数，
∴t(x)min＝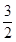
(1－1)＝0.∴a≤0.
(2)由题意，得f′(3)＝0，
即27－6a－3＝0，
∴a＝4.∴f(x)＝x3－4x2－3x，
f′(x)＝3x2－8x－3.
令f′(x)＝0，得x1＝－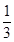
，x2＝3.
当x变化时，f′(x)、f(x)的变化情况如下表：
| x | 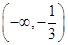| 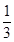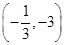－ | | 3 | (3，＋∞) |
| f′(x) | ＋ | 0 | － | 0 | ＋ |
| f(x) | | 极大值 | | 极小值 | |
∴f(x)的单调递增区间为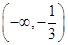，[3，＋∞)，f(x)的单调递减区间为.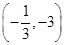