问题
解答题
一个倒圆锥形容器,它的轴截面是正三角形,在容器内注入水,并放入一个半径为r的铁球,这时水面恰好与球的上面相切,将球从圆锥内取出后,求圆锥内的水深.
答案
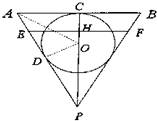
如图.在容器内注入水,并放入一个半径为r的铁球,这时水面记为AB,
将球从圆锥内取出后,这时水面记为EF.
三角形PAB为轴截面,是正三角形,
三角形PEF也是正三角形,圆O是正三角形PAB的内切圆.
由题意可知,DO=CO=r,AO=2r=OP,AC=
r,3
∴V球=
πr3,VPC=4 3
π(1 3
r)2?3r=3πr33
又设HP=h,则EH=
h3 3
∴V水=
π(1 3
h)2?h=3 3
h3π 9
∵V水+V球=VPC
即
h3+π 9
πr3=3πr3,4 3
∴h=
r3 15
即圆锥内的水深是
r.3 15
