问题
选择题
正方体ABCD-A1B1C1D1中,面对角线BC1与对角面BB1D1D所成角的正切值( )
|
答案
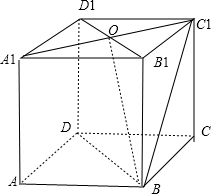
连接A1C1,设A1C1 ∩B1D1=O,连接BO,则A1C1 ⊥B1D1,
∵ABCD-A1B1C1D1是正方体
∴BB1⊥A1C1,
∵BB1∩B1D1=B1,
∴C1O⊥平面B1D1DB
∴∠C1BO为面对角线BC1与对角面BB1D1D所成角
设棱长为2,则BC1=2
,C1O=2 2
∴∠C1BO=30°
∴面对角线BC1与对角面BB1D1D所成角的正切值为3 3
故选C
