问题
填空题
过棱长为2的正方体AC1的棱AD、CD、A1B1的中点E、F、G作一截面,则△EFG的面积为______,点B到平面EFG的距离为______.
答案
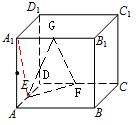
连接A1E,在直角三角形AA1E中,A1E=
=AA12+AE2
=22+12
,5
在直角三角形A1EG中,GE=
=A1E2+A1G2
=5+1
,6
同理,FG=2
,EF=2
,有EG2+EF2=GF2,∴∠GEF=90°,2
∴△EFG的面积为
EG×EF=1 2
×1 2
×6
=2
.3
设B到平面EFG距离为h,
根据VB-EFG=VG-EFB,可得
×1 3
×h=3
×1 3
×1 2
×2
×23 2 2
∴h=
.3
故答案为:
,3
.3
