由函数f(x)=

1

3

x3+

1

2

ax2+2bx(a，b∈R)可得，

f'（x）=x²+ax+2b，…（2分）

由题意知，α，β是方程x²+ax+2b=0的两个根，…（5分）

且α∈（0，1），β∈（1，2），

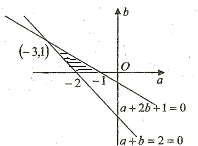
因此得到可行域

f′(0)=2b＞0 f′(1)=1+a+26＜0 f′(2)=4+2a+2b＞0

…（9分）

即

b＞0 a+2b+1＜0 a+b+2＞0

，画出可行域如图．…（11分）

所以S=

1

2

×1×1=

1

2

…（12分）；