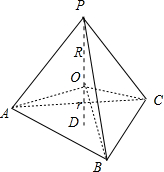
设正四面体为PABC，两球球心重合，设为O．

设PO的延长线与底面ABC的交点为D，则PD为正四面体PABC的高，PD⊥底面ABC，

且PO=R，OD=r，OD=正四面体PABC内切球的高．

设正四面体PABC底面面积为S．

将球心O与四面体的4个顶点PABC全部连接，

可以得到4个全等的正三棱锥，球心为顶点，以正四面体面为底面．

每个正三棱锥体积V₁=

1

3

?S?r 而正四面体PABC体积V₂=

1

3

?S?（R+r）

根据前面的分析，4?V₁=V₂，

所以，4?

1

3

?S?r=

1

3

?S?(R+r)，

所以，

r

R

=

1

3

．

故选B．