问题
选择题
三棱锥P-ABC中，若PA=PB=PC，则顶点P在底面三角形的射影是底面三角形的（ ）
A．内心
B．外心
C．重心
D．垂心
答案
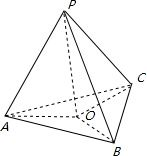
设点P作平面ABC的射影为O，
连接OA，OB，OC，
∵三棱锥的三条侧棱两两相等，
∴PA=PB=PC，
∵PO⊥底面ABC，
PO⊥OA，PO⊥OB，PO⊥OC，
∴△PAO≌△POB≌△POC
∴OA=OB=OC
所以O为三角形的外心．
故选B．
搜题请搜索小程序“爱下问搜题”