问题
选择题
设f（x），g（x）分别是定义在R上的奇函数和偶函数．当x＜0时，f'（x）g（x）+f（x）g'（x）＞0，且g（-3）=0，则不等式
|
答案
解：设F（x）=f （x）g（x），当x＜0时，
∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0，
∴F（x）在（-∞，0）上为增函数；
∵F（-x）=f （-x）g （-x）=-f （x）?g （x）=-F（x），
∴F（x）为R上的奇函数，故F（x）在R上亦为增函数．
∵g（-3）=0，必有F（-3）=F（3）=0．
构造如图的F（x）=f （x）g（x）的图象，
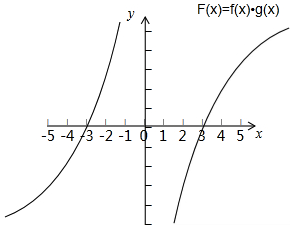
可知F（x）＞0的解集为（-3，0）∪（3，+∞）．
∴
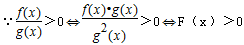
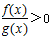的解集就是F（x）＞0的解集（-3，0）∪（3，+∞）．
故选A．
