问题
填空题
若正六棱锥P-ABCDEF的侧棱PA与底边BC成45°角，底面边长为a，则对角面面积最大的值是______．
答案
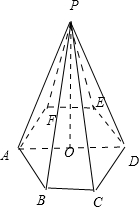
作PO⊥底面ABCDEF，交AD于O，
∵正六棱锥P-ABCDEF的侧棱PA与底边BC成45°角，
∴∠PAO=45°．
∵底面边长为a，
∴AO=PO=a，
AD=2a，
∴对角面面积最大的值：
S=S△PAB=
AD•PO=1 2
×2a×a=a2．1 2
故答案为：a2．
搜题请搜索小程序“爱下问搜题”