如图(a),平行金属板A和B间的距离为d,现在A、B板上加上如图(b)所示的方波形电压,t=0时A板比B板的电势高,电压的正向值为U0,反向值也为U0.现有由质量为m的带正电且电荷量为q的粒子组成的粒子束,从AB的中点O以平行于金属板方向OO′的速度v0=射入,所有粒子在AB间的飞行时间均为T,不计重力影响.求:
(1)粒子飞出电场时的速度;
(2)粒子飞出电场时位置离O′点的距离范围
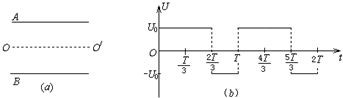
(1)将粒子的运动沿着平行于初速度方向和垂直于初速度的方向正交分解,在平行于初速度方向,粒子做匀速直线运动,有
v∥=v0=
在垂直于初速度方向,粒子在电场力的作用下做变速直线运动,根据牛第二定律,有
a==
任意时刻进入后,穿过电场的时间都为T,故
v⊥=a•T-a•T=aT
故
v⊥=
故飞出电场时的速度为v==.
(2)粒子在t=0、T、2T…时刻进入时,O′位置偏向最下端,此时,在垂直电场方向,粒子先向下匀加速直线运动后向下匀减速直线运动,根据运动学公式,有
y1=[•a•()2]+[a•()]•(T)-•a•(T)2=
粒子在t=、+T、+2T…时刻进入时,O′位置偏向最上端,此时,在垂直电场方向,粒子先向上匀加速直线运动后向上匀减速直线运动最后向下匀加速直线运动,根据运动学公式,有
y2=[•a•(T)2]+[a•(T)]•()-•a•()2=
故粒子飞出电场时位置在O′点的上方到下方范围内.

