半径为r=0.5m带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面的平行金属板连接,两板间距离为d=5cm,如图甲所示,有变化的磁场垂直于纸面,其变化规律如图乙所示(规定向里为正方向),在t=0时刻平板间中心有一电荷量为+q的微粒由静止释放,运动中粒子不碰板,不计重力作用,则以下说法中正确的是( )
A.第2秒内上极板带负电
B.第3秒内上极板带正电
C.第3秒末微粒回到了原位置
D.两极板之间的电场强度大小恒为πN c 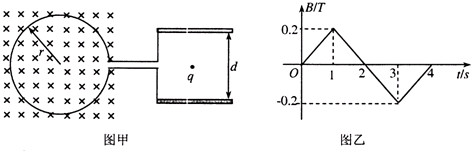
根据法拉第电磁感应定律可知圆环中的感应电动势为:E=
=s△Φ △t
,根据图乙可知:B-t图象中的斜率保持不变,因此感应电动势的大小不变.△B △t
根据B-t图可知,1s到3s这段时间内感应电动势大小不变,根据楞次定律可知感应电流方向为逆时针,因此上极板带正电,故A错误,B正确;
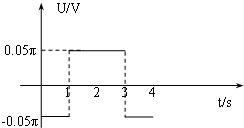
代入数据可求出电动势的大小为:E=0.05π(V),随时间变化如下图所示(上极板电势为正):
所以粒子先向上加速1s,然后向上减速1s,接着反向加速1s,因此第3秒末微粒并未回到原位置,故C错误;
根据电场强度与电势差的关系有:E=
=U d
=π(N/C),故D正确.0.05π 0.05
故选BD.

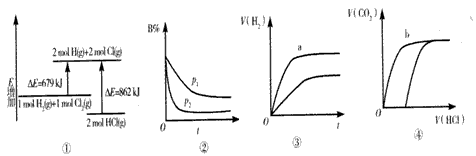
 2C(g)+6D(?)在不同压强下B%随时间的变化,则D一定是气体
2C(g)+6D(?)在不同压强下B%随时间的变化,则D一定是气体