问题
填空题
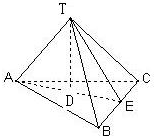
| 已知在三棱锥T-ABC中,TA,TB,TC两两垂直,T在地面ABC上的投影为D,给出下列命题: ①TA⊥BC,TB⊥AC,TC⊥AB; ②△ABC是锐角三角形; ③
④
其中正确的是______(写出所有正确命题的编号). |
答案
对于①,TA,TB,TC两两垂直可得:TA⊥平面TBC,从而得出:TA⊥BC,同理得到TB⊥AC,TC⊥AB,故①正确;
②设TA=a;TB=b;TC=c,则AB2=a2+b2,同理BC2=c2+b2,Ac2=a2+c2,在三角形ABC中,由余弦定理得:cosA=
=AB2+AC2-BC2 2AB×AC
=a2+b2+a2+c2-c2-b2 2 a2+b2 a2+c2
>0,同理可证cosB>0,cosC>0,所以,)△ABC是锐角三角形.a2 a2+b2 a2+c2
③设TA=a;TB=b;TC=c,在直角三角形TBC中,得:TE=
,bc b2+c2
在三角形ABC中,有:AE=a2b2+b2c2+c2a2 b2+c2
由于AE×TD=TA×TE
∴
×TD=a×a2b2+b2c2+c2a2 b2+c2
,bc b2+c2
∴a2b2c2=(a2b2+b2c2+c2a2)TD 2
∴
=1 TD2
+1 TA2
+1 TB2
;成立1 TC2
故③对
④:S△BCA2=S△TBC2+S△ACT2+S△TAB2.证明如下:
如图作TE⊥CB于E,连AE,则AE⊥CB.
S△BCA2 =
BC2•AE2 =1 4
BC2•(AT2+TE2)=1 4
(TB2+TC2)(AT2+TE2)1 4
=
(TB2TC2 +TA2TC2+TA2TB2 )=S△TBC2+S△ACT2+S△TAB2,1 4
故不对;
故答案为:①②③.