问题
解答题
设函数f(x)的导函数为f′(x),若f(x)=ax3-ax2+[
(1)a表示f′(1); (II)若函数f(x)f在R上存在极值,求a的范围. |
答案
(I)f′(x)=3ax2-2ax+
-1,f′(1) 2
把x=1代入上式得f′(1)=a+
-1,f′(1) 2
所以f′(1)=2a-2;
(II)由(1)可知:f′(x)=3ax2-2ax+a-2,
a=0时,f′(x)=-2<0,所以f(x)在R上单调递减,无极值;
当a≠0时,若函数f(x)f在R上存在极值,则f′(x)=0必须有两个相异根.
故△>0,即4a2-4×3a×(a-2)>0,
即4a2-12a(a-2)>0,
解得0<a<3.

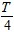 时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )
时(T为交流的周期),原线圈中的电流瞬时值为0.03A.变压器的原、副线圈的匝数比为( )
 :3
:3