问题
解答题
如图，四边形ABCD为矩形，DA⊥平面ABE，
AE=EB=BC=2，EB⊥平面ACE于点F，且点F在CE上。
（1）求证：AE⊥BE；（2）求三棱锥D—AEC的体积；
（3）设点M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN//平面DAE。
答案
(Ⅰ)略 (Ⅱ)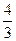 
（Ⅲ）当点N为线段CE上靠近点C的一个三等分点
解（1）证明：则AD⊥平面ABE成AD//BC得BC⊥平面ABE，则AE⊥BC
而BF⊥平面ACE，则BF⊥AE，又BC∩⊥BF=B，则AE⊥平面BCE，又BE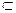
平面BCE，故AE⊥BE。…1分
（2）在△ABE中，过点E作EH⊥AB于点H，则EH⊥平面ACD。
由已知及（1）得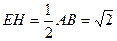
，
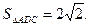……………………2分
故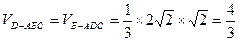
……………………1分
（3）当点N为线段CE上靠近点C的一个三等分点时，MN//平面ADE。…………1分
取线段BE上靠近点B的一个三等分点G，连接MN，MG，NG
则由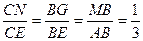
得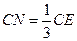
，则MG//AE GN//BC
由MG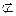
平面ADE，AE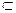平面ADE,则MG//面ADEMG∩NG=G，同理,得GN//面ADE,MG
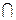NG=G平面ADE//面MNG又MN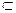平面MGN，则MN//平面ADE。
故当点N为线段CE上靠近点C的一个三等分点时，MN//平面ADE。