问题
解答题
等边ABC的A∈平面α，B、C到面α的距离分别为2a、a，且AB=BC=AC=b.
(1)求面ABC与α所成二面角的大小；
(2)若B、C到α的距离分别为3a、a呢?
答案
（1）∠BAG=arcsin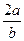
（2）arcsin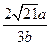
(1)延长BD交α于D B、C在α上的射影为G、H.则
G、H、D共线 BG="2GH " ∴BC=CD
∴∠BAD=90°,GA⊥AD,∠BAG为所求.
sin∠BAC=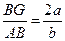
∠BAG=arcsin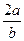
(2)
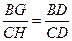=3
∴BC="2CD " CD=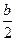
AD2=AC2+CD2+AC·CD=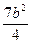
∴AD=
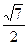b
C到AD的距离为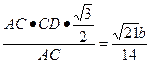
设所成角为α，则
sinα=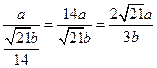
α=arcsin