问题
填空题
对于四面体ABCD,以下命题中,真命题的序号为 (填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
答案
①②④.
题目分析:①正确.由已知可得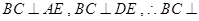 平面
平面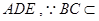 平面
平面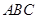 ,故平面
,故平面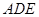 ⊥平面
⊥平面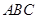 ;②正确.如图,作
;②正确.如图,作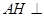 平面
平面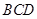 于
于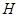 ,连结
,连结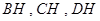 .
.
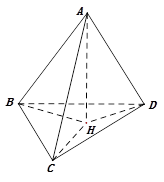
则 平面
平面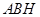 ,
,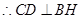 .同理可证
.同理可证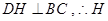 为
为 的垂心,
的垂心,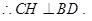 又
又 面
面 .③错误.若所有棱长都相等,则该四面体的外接球与内切球的半径之比为3:1;④正确.如图,作
.③错误.若所有棱长都相等,则该四面体的外接球与内切球的半径之比为3:1;④正确.如图,作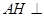 平面
平面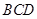 于
于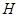 ,连结
,连结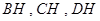 .则
.则
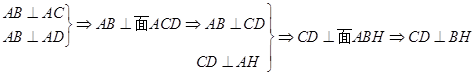
同理可证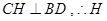 为
为 的垂心.分别作两组相对棱中点的连线,则所得的两条直线交于一点.故⑤错误.
的垂心.分别作两组相对棱中点的连线,则所得的两条直线交于一点.故⑤错误.
