问题
解答题
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100)，已知成绩在90分以上(含90分)的学生有13人．
(1)求此次参加竞赛的学生总数共有多少人？
(2)若计划奖励竞赛成绩排在前228名的学生，问受奖学生的分数线是多少？
答案
(1) 10000人 (2) 80分
解：(1)设学生的成绩为X，共有n人参加竞赛，
∵X～N(60,100)，∴μ＝60，σ＝10.
∴P(X≥90)＝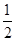
[1－P(30＜X＜90)]
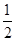＝(1－0.9974)＝0.0013.
又P(X≥90)＝
，∴＝0.0013.∴n＝10000.
故此次参加竞赛的学生总数共有10000人．
(2)设受奖的学生的分数线为x0.
则P(X≥x0)＝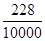
＝0.0228.
∵0.0228＜0.5，∴x0＞60.
∴P(120－x0＜X＜x0)＝1－2P(X≥x0)＝0.9544，
∴x0＝60＋20＝80.故受奖学生的分数线是80分．
