问题
证明题
已知α1,α2,…αn∈(0,π),n是大于1的正整数,
求证:|sin(α1+α2+…+αn)|<sinα1+sinα2+…+sinαn。
答案
k
| 解:下面用数学归纳法证明 |
①n=2时,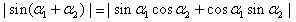 |
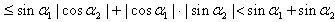 |
| 所以n=2时成立; |
| ②假设n=k(k≥2)时成立,即 |
|sin(α1+α2+…+αn)|<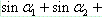 …+sinak …+sinak |
当n=k+1时,|sin(α1+α2+…+αk+1)|=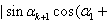 …+ …+ …+ak)| …+ak)| |
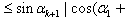 …+ak)|+ …+ak)|+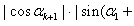 …+ak)| …+ak)| |
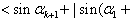 …+ak)| …+ak)| |
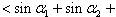 …+ …+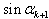 |
| ∴n=k+1时也成立。 |
由①②得,原式成立。
