问题
解答题
| 在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某明星判断正确的概率为p,判断错误的概率为q,若判断正确则加1分,判断错误则减1分,现记“该明星答完n题后总得分为Sn”. (1)当p=q=
(2)当p=
|
答案
(1)∵ξ=|S3|的取值为1,3,又p=q=
;1 2
∴P(ξ=1)=2
(C 13
)•(1 2
)2=1 2
,3 4
P(ξ=3)=(
)3+(1 2
)3=1 2
.1 4
∴ξ的分布列为:
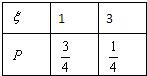
∴Eξ=1×
+3×3 4
=1 4
;3 2
Dξ=
×(1-3 4
)2+3 2
×(3-1 4
)2=3 2 3 4
(2)当S 8=2时,即答完8题后,回答正确的题数为5题,回答错误的题数是3题,
又已知Si≥0(i=1,2,3,4),若第一题和第二题回答正确,则其余6题可任意答对3题;
若第一题正确,第二题回答错误,第三题回答正确,则后5题可任意答对3题.
此时的概率为P=(
+C 36
)•(C 35
)5•(1 3
)3=2 3
=30×8 38
(或80 37
).80 2187
