求证:无论x、y为何值,4x2-12x+9y2+30y+35的值恒为正。
解:原式=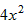 -12x+9+
-12x+9+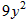 +30y+25+1
+30y+25+1
=(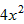 -12x+9)+(
-12x+9)+(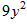 +30y+25)+1
+30y+25)+1
=[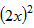 -2×2x×3+32]+[(3y)2+2×3y×5+52]+1
-2×2x×3+32]+[(3y)2+2×3y×5+52]+1
=(2x-3)2+(3y+5)2+1
因为(2x-3)2≥0,(3y+5)2≥0,所以(2x-3)2+(3y+5)2+1≥1
即4x2-12x+9y2+30y+35的值恒为正。
求证:无论x、y为何值,4x2-12x+9y2+30y+35的值恒为正。
解:原式=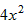 -12x+9+
-12x+9+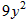 +30y+25+1
+30y+25+1
=(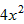 -12x+9)+(
-12x+9)+(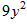 +30y+25)+1
+30y+25)+1
=[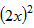 -2×2x×3+32]+[(3y)2+2×3y×5+52]+1
-2×2x×3+32]+[(3y)2+2×3y×5+52]+1
=(2x-3)2+(3y+5)2+1
因为(2x-3)2≥0,(3y+5)2≥0,所以(2x-3)2+(3y+5)2+1≥1
即4x2-12x+9y2+30y+35的值恒为正。