问题
解答题
某校要组建明星篮球队,需要在各班选拔预备队员,规定投篮成绩A级为入围选手,选拔过程中每人投篮5次,若投中3次确定为B级,若投中4次以上可确定为A级,已知某班同学阿明每次投篮投中的概率为0.5.
(1)求阿明投篮4次才被确定为B级的概率;
(2)设阿明投篮投中的次数为X,求X的分布表及期望;
(3)若连续两次投篮不中则停止投篮,求阿明不能入围的概率.
答案
(1)阿明投篮4次才被确定为B级的概率
P=
(C 23
)2×1 2
×1 2
=1 2
.(2分)3 16
(2)由已知x~B(5,
),X的分布列为:1 2
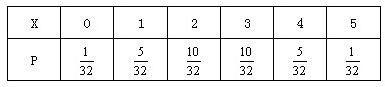
E(X)=
.(4分)5 2
(3)若连续两次投篮不中则停止投篮,
阿明不能入围这一事件有如下几种情况:
①5次投中3次,有C42+1种投球方式,
其概率为P(3)=(
+1)(C 24
)5=1 2
;(5分)7 32
②投中2次,分别是中中否否、
中否中否否、否中中否否、否中否中否,
概率是:P(2)=(
)4+3×(1 2
)5=1 2
;(7分)5 32
③投中1次分别有中否否、否中否否,
概率为:P(1)=(
)3+(1 2
)4=1 2
10;(8分)3 16
④投中0次只有否否一种,
概率为P(0)=(
)2=1 2
;(9分)1 4
所以阿明不能入围这一事件的概率是:
P=P(3)+P(2)+P(1)+P(0)=
.(10分)13 16