问题
问答题
某司机在平直公路上测试汽车的制动性能。他从车上速度表看到汽车速度的大小为v=72km/h时紧急刹车,由于车轮与公路面的摩擦,车轮在公路面上划出一道长L=40m的刹车痕迹后停止。求:
(1)车轮与公路面间的动摩擦因数μ;
(2)该司机驾车仍以v=72km/h的速度在一段动摩擦因数也为μ、倾角为8°的坡路上匀速
向下行驶,发现前方停着一辆故障车。若刹车过程司机的反应时间为△t=0.7s,为了避免两
车相撞,该司机至少应在距故障车多远处采取同样的紧急刹车措施?
(取sin8°="0.14," cos8°=0.99,g=10m/s2)
答案
(1)0.5(2)70.3m
(1)汽车做匀减速运动而停止,初速度v=72km/h=20m/s
由vt2 – v02 =" 2as" 得 -v2=2al
由牛顿第二定律 -μmg=ma
由①②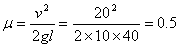
(2)在反应时间△t内,汽车仍做匀速运动,其位移
s1=v·△t=20×0.7m=14m
实施紧急刹车后,汽车的加速度为a′,由牛顿第二定律得
mgsin8°-μmgcos8°=m a′
a′=g(sin8°-μcos8°)=10×(0.14-0.5×0.99)m/s2=-3.55m/s2
此时间内汽车位移为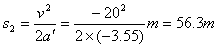
则两车车距至少应为s=s1+s2=(14+56.3)m=70.3m
