问题
填空题
正四棱锥S－ABCD的底面边长为2，高为2，E是边BC的中点，动点P在棱锥表面上运动，并且总保持PE⊥AC，则动点P的轨迹的周长为________．
答案
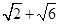
联结AC，BD交于点O，联结SO，则SO⊥平面ABCD，由AC平面ABCD，故SO⊥AC.取SC中点F和CD中点G，联结GF，FE，GE，GE交AC于H，则H为OC的中点，故FH∥SO，则FH⊥AC，又由GE∥BD，BD⊥AC得GE⊥AC.∵GE∩FH＝H，GE，FH平面FGE，∴AC⊥平面FGE，故当P∈平面FGE时，总有PE⊥AC，故动点P的轨迹即为△FGE的周长，求得结果为.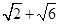
vBl
vBl