问题
解答题
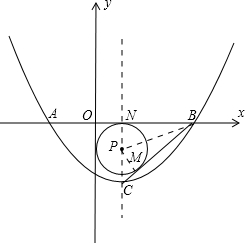
在直角坐标系中,抛物线y=
(1)求此抛物线的解析式和经过B,C两点的直线的解析式; (2)点P在此抛物线的对称轴上,且⊙P与x轴、直线BC都相切.求点P的坐标. |
答案
(1)设A点的坐标为(-a,0),则B点的坐标为(2a,0),其中a>0.
由题意得一元二次方程0=
x2+4 9
mx+2 9
m+5 9
,4 3
那么
⇒2m2-5m-12=0,-a+2a= -
m2 9 - 4 9 -a•2a=
m+5 9 4 3 - 4 9
解得m=-
(不合题意舍去),3 2
m=4,则a=2,
∴此抛物线的解析式为y=
(x-1)2-4,4 9
B点的坐标为(4,0)、C点的坐标为(1,-4),
∴经过B,C两点的直线的解析式为y-0=
(x-4),-4-0 1-4
即y=
x-4 3
;16 3
(2)∵点P在此抛物线的对称轴上,故设P点的坐标为(1,k),
设⊙P与x轴、直线BC分别相切于点N、M,连接PB、PM,
在△PBC中,BC=
=NB2+NC2
=5,32+42
S△PBC=
PC•NB=1 2
BC•PM,1 2
即PM=
,[k-(-4)]•3 5
∵PM、NP均为圆P的半径,
∴|k|=
,(k+4)•3 5
解得k=6(不合题意舍去),k=-
,3 2
∴P点的坐标为(1,-
).3 2