对于三次函数f(x)=ax3+bx2+cx+d,定义y=f″(x)是函数y=f′(x)的导函数.若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现:任何一个三次函数既有拐点,又有对称中心,且拐点就是对称中心.根据这一发现,对于函数g(x)=
|
令h(x)=
x3-1 3
x2+3x+1 2
,则h′(x)=x2-x+3,h″(x)=2x-1,1 12
令h″(x)=0,解得x=
,又h(1 2
)=1 2
,∴函数h(x)的拐点为(3 2
,1 2
),即为函数h(x)的对称中心..3 2
∴h(
)+h(1 2013
)=2h(2012 2013
)=3.1 2
∴g(
)+g(1 2013
)+g(2 2013
)+…+g(3 2013
)=3×1006=3018.2012 2013
设u(x)=
,可知其图象关于点(1 x- 1 2
,0)中心对称.1 2
∴u(
)+u(1 2013
)=0=u(2012 2013
)+u(2 2013
)=…,2011 2013
∴u(
)+u(1 2013
)+…+u(2 2013
)=0.2012 2013
∴g(
)+g(1 2013
)+g(2 2013
)+…+g(3 2013
)=3018.2012 2013
故答案为3018.

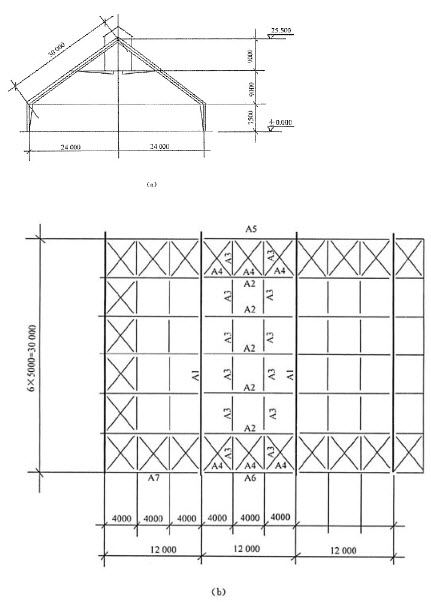
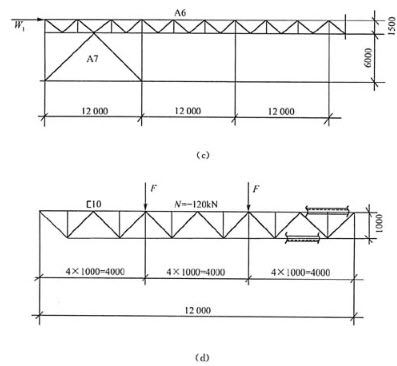
 按近似方法计算,取βtx=0.65。
按近似方法计算,取βtx=0.65。