问题
解答题
已知二次函数y=
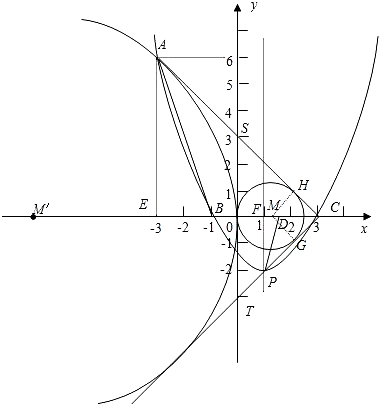
(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象; (2)设D为线段OC上的一点,满足∠DPC=∠BAC,求点D的坐标; (3)在x轴上是否存在一点M,使以M为圆心的圆与AC、PC所在的直线及y轴都相切?如果存在,请求出点M的坐标;若不存在,请说明理由. |
答案
(1)∵二次函数y=
x2+bx+c的图象过点A(-3,6),B(-1,0),1 2
得
,
-3b+c=69 2
-b+c=01 2
解得
.b=-1 c=- 3 2
∴这个二次函数的解析式为:
y=
x2-x-1 2
.(4分)3 2
由解析式可求P(1,-2),C(3,0),(5分)
画出二次函数的图象;(6分)
(2)解法一:
易证:∠ACB=∠PCD=45°,
又已知:∠DPC=∠BAC,
∴△DPC∽△BAC,(8分)
∴
=DC BC
,PC AC
易求AC=6
,PC=22
,BC=4,2
∴DC=
,4 3
∴OD=3-
=4 3
,5 3
∴D(
,0).(10分)5 3
解法二:过A作AE⊥x轴,垂足为E,
设抛物线的对称轴交x轴于F,
亦可证△AEB∽△PFD,(8分)
∴
=PE PF
,EB FD
易求:AE=6,EB=2,PF=2,
∴FD=
,2 3
∴OD=
+1=2 3
,5 3
∴D(
,0);(10分)5 3
(3)存在.
①过M作MH⊥AC,MG⊥PC垂足分别为H、G,设AC交y轴于S,CP的延长线交y轴于T,
∵△SCT是等腰直角三角形,M是△SCT的内切圆圆心,
∴MG=MH=OM,(11分)
又∵MC=
OM且OM+MC=OC,2
∴
OM+OM=3,2
得OM=3
-3,2
∴M(3
-3,0)(12分)2
②在x轴的负半轴上,存在一点M′,
同理OM′+OC=M′C,OM′+OC=
OM′2
得OM′=3
+32
∴M′(-3
-3,0)(14分)2
即在x轴上存在满足条件的两个点.