问题
解答题
抛物线y=ax2+bx+c经过点(-1,0),(3,0)(0,-3),求它的开口方向、对称轴和顶点坐标,并画出草图.
答案
解法一:把(-1,0),(3,0),(0,-3),代入y=ax2+bx+c,得:
,a-b+c=0 9a+3b+c=0 c=-3
解得:
,a=1 b=-2 c=-3
则函数解析式为y=x2-2x-3,即y=(x-1)2-4,
∴开口向上,对称轴为x=1,顶点坐标为(1,-4);
解法二:设函数的解析式为y=a(x+1)(x-3),
把(0,-3)代入得函数的解析式为y=(x+1)(x-3),
即y=x2-2x-3,写成顶点式y=(x-1)2-4,
∴开口向上,对称轴为x=1,顶点坐标为(1,-4).
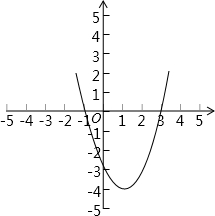
草图为: