问题
解答题
已知函数f（x）=﹣x3+ax在（0，1）上是增函数．
（1）求实数a的取值范围A；
（2）当a为A中最小值时，定义数列{an}满足：a1=b∈（0，1），且2an+1=f（an），试比较an与an+1的大小．
答案
解：（1）∵f（x）=﹣x3+ax，
∴f′（x）=﹣3x2+a，
∵f（x）=﹣x3+ax在（0，1）上是增函数，
∴f′（1）=﹣3+a≥0，
∴a≥3，即A=[3，+∞）．
（2）当a=3时，由题意：an+1= 
f（an）=﹣ 
+ 
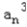an，且a1=b∈（0，1），
以下用数学归纳法证明：an∈（0，1），对n∈N*恒成立．
①当n=1时，a1=b∈（0，1）成立；
②假设n=k时，ak∈（0，1）成立，
那么当n=k+1时， ak+1=﹣
ak3+ 
ak，
由①知g（x）=（﹣x3+3x）在（0，1）上单调递增，
∴g（0）＜g（ak）＜g（1）即0＜ak+1＜1，
由①②知对一切n∈N*都有an∈（0，1）
而an+1﹣an=﹣
an3+ 
an﹣an= 
an（1﹣an2）＞0
∴an+1＞an．