（I）f'（x）=x²-2ax-3a²．（3分）

（Ⅱ）令f'（x）=x²-2ax-3a²=0，得x=-a或x=3a．（5分）

则当x变化时，f（x）与f'（x）的变化情况如下表：

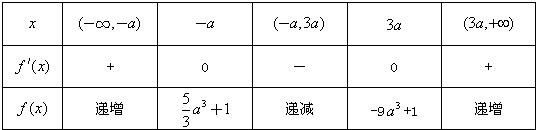
可知：当x∈（-∞，-a）时，函数f（x）为增函数，当x∈（3a，+∞）时，函数f（x）也为增函数．（6分）

当x∈（-a，3a）时，函数f（x）为减函数．（7分）当x=-a时，f(x)的极大值为

5

3

a3+1；（8分）

当x=3a时，f（x）的极小值为-9a³+1．（9分）

（Ⅲ）因为f'（x）=x²-2ax-3a²的对称轴为x=a，

且其图象的开口向上，所以f'（x）在区间[a+1，a+2]上是增函数．（10分）

则在区间[a+1，a+2]上恒有f'（x）＞-3a等价于f'（x）的最小值大于-3a成立．

所以f'（a+1）=（a+1）²-2a（a+1）-3a²=-4a²+1＞-3a．（12分）

解得-

1

4

＜a＜1．又a＞0，故a的取值范围是（0，1）