（1）证明：①当k=0时，方程为x+3=0，所以x=-3，方程有实数根，

②当k≠0时，△=（3k+1）²-4k•3，

=9k²+6k+1-12k，

=9k²-6k+1，

=（3k-1）²≥0，

所以，方程有实数根，

综上所述，无论k取任何实数时，方程总有实数根；

（2）令y=0，则kx²+（3k+1）x+3=0，

解关于x的一元二次方程，得x₁=-3，x₂=-

1

k

，

∵二次函数的图象与x轴两个交点的横坐标均为整数，且k为正整数，

∴k=1；

（3）由（2）得抛物线的解析式为y=x²+4x+3，

配方得y=（x+2）²-1，

∴抛物线的顶点M（-2，-1），

∴直线OD的解析式为y=

1

2

x，

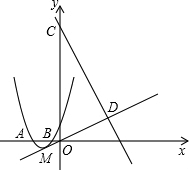
于是设平移后的抛物线的顶点坐标为（h，

1

2

h），

∴平移后的抛物线解析式为y=（x-h）²+

1

2

h，

①当抛物线经过点C时，令x=0，则y=9，

∴C（0，9），

∴h²+

1

2

h=9，

解得h=

-1± 145

4

，

∴当

-1- 145

4

≤h＜

-1+ 145

4

时，平移后的抛物线与射线CD只有一个公共点；

②当抛物线与直线CD只有一个公共点时，

由方程组

y=(x-h)2+ 1 2 h y=-2x+9

，

消掉y得，x²+（-2h+2）x+h²+

1

2

h-9=0，

∴△=（-2h+2）²-4（h²+

1

2

h-9）=0，

解得h=4，

此时抛物线y=（x-4）²+2与射线CD唯一的公共点为（3，3），符合题意，

综上所述：平移后的抛物线与射线CD只有一个公共点时，顶点横坐标的值或取值范围是h=4或

-1- 145

4

≤h＜

-1+ 145

4

．