问题
解答题
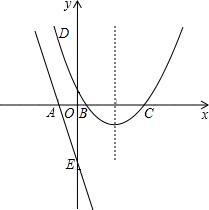
在平面直角坐标系中,给定以下五点A(-2,0)、B(1,0)、C(4,0)、D(-2,
我们约定:把经过三点A、E、B的抛物线表示为抛物线AEB. (1)问符合条件的抛物线还有哪几条?不求解析式,请用约定的方法一一表示出来; (2)在(1)中是否存在这样的一条抛物线,它与余下的两点所确定的直线不相交?如果存在,试求出抛物线及直线的解析式并证明;如果不存在,请说明理由. |
答案
(1)符合条件的抛物线还有5条,分别如下:
①抛物线AEC;
②抛物线CBE;
③抛物线DEB;
④抛物线DEC;
⑤抛物线DBC.
(2)在(1)中存在抛物线DBC,它与直线AE不相交.
设抛物线DBC的解析式为y=ax2+bx+c,
将D(-2,
),B(1,0),C(4,0)三点坐标分别代入,9 2
得:4a-2b+c=
,a+b+c=0,9 2
即16a+4b+c=0,
解这个方程组,得:a=
,b=-1 4
,c=1,5 4
∴抛物线DBC的解析式为y=
x2-1 4
x+1.5 4
另法:设抛物线为y=a(x-1)(x-4),代入D(-2,
),得a=9 2
也可.1 4
又设直线AE的解析式为y=mx+n.将A(-2,0),E(0,-6)两点坐标分别代入,
得:-2m+n=0,n=-6.
解这个方程组,得m=-3,n=-6.
∴直线AE的解析式为y=-3x-6.