问题
解答题
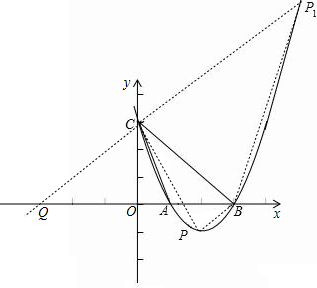
已知抛物线y=x2-4x+3与x轴交于两点A、B(A在B左侧),与y轴交于点C.
(1)对于任意实数m,点M(m,-3)是否在该抛物线上?请说明理由;
(2)求∠ABC的度数;
(3)若点P在抛物线上,且使得△PBC是以BC为直角边的直角三角形,试求出点P的坐标.
答案
(1)假如点M(m,-3)是在该抛物线上,
∴-3=m2-4m+3,
∴m2-4m+6=0.
∴△=(-4)2-4×1×6=-8<0,
∴此方程无实数解,
∴对于任意实数m,点M(m,-3)是不在该抛物线上.
(2)当y=0时,x2-4x+3=0,
∴x1=1,x2=3,由于点A在点B的左侧,
∴A(1,0),B(3,0).
当x=0时,y=3,
∴C(0,3),
∴OB=OC=3.
∵∠COB=90°,
∴∠OBC=∠OCB=45°,
即∠ABC=45°.
(3)假设存在△PBC是以BC为直角边的直角三角形.当∠PBC=90°时,∵∠ABC=45°,
∴∠PBO=45°,
∴P(2,-1);
当∠PCB=90°时,设直线PC交x轴于Q,
∵∠ABC=45°,
∴∠BQC=45°,
∴OQ=OC=3,Q(-3,0),
设直线PC的解析式为y=kx+b,则,
,3=b 0=-3k+b
∴
,k=1 b=3
∴直线的解析式为:y=x+3.
∵点P在抛物线上,
∴
,y=x+3 y=x2-4x+3
解得.x1=0(舍去),x2=5
∴当x=5时,y=8,此时P1(5,8)
∴存在点P(2,-1)或(5,8)使得△PBC是以BC为直角边的直角三角形.