比较下列各组中两个代数式的大小:
(1)x2+3与3x ;
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2。
解:(1)x2+3-3x=x2-3x+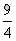 -
-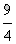 +3=(x-
+3=(x-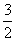 )2+
)2+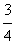 >0,
>0,
∴x2+3>3x。
(2)a3+b3-(a2b+ab2)=a2(a-b)+b2(b-a)=(a2-b2)(a-b)=(a-b)2(a+b),
∵a,b为正数,且a≠b,
∴(a-b)2>0,a+b>0,
∴(a-b)2(a+b)>0,
∴a3+b3>a2b+ab2。
比较下列各组中两个代数式的大小:
(1)x2+3与3x ;
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2。
解:(1)x2+3-3x=x2-3x+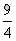 -
-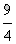 +3=(x-
+3=(x-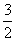 )2+
)2+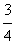 >0,
>0,
∴x2+3>3x。
(2)a3+b3-(a2b+ab2)=a2(a-b)+b2(b-a)=(a2-b2)(a-b)=(a-b)2(a+b),
∵a,b为正数,且a≠b,
∴(a-b)2>0,a+b>0,
∴(a-b)2(a+b)>0,
∴a3+b3>a2b+ab2。