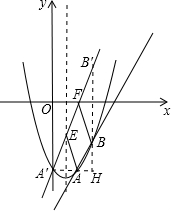
已知二次函数y=x2-mx+m-2.
(1)求证:无论m为任何实数,该二次函数的图象与x轴都有两个交点;
(2)当该二次函数的图象经过点(3,6)时,求二次函数的解析式;
(3)将直线y=x向下平移2个单位长度后与(2)中的抛物线交于A、B两点(点A在点B的左边),一个动点P自A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.
(1)证明:令y=0,则x2-mx+m-2=0,
∵△=(-m)2-4(m-2)=m2-4m+8=(m-2)2+4,(1分)
又∵(m-2)2≥0,
∴(m-2)2+4>0,即△>0.
∴无论m为任何实数,一元二次方程x2-mx+m-2=0总有两不等实根;
∴该二次函数图象与x轴都有两个交点.(2分)
(2)∵二次函数y=x2-mx+m-2的图象经过点(3,6),
∴32-3m+m-2=6,
解得m=
;1 2
∴二次函数的解析式为y=x2-
x-1 2
.(3分)3 2
(3)将y=x向下平移2个单位长度后得到解析式为:y=x-2,(4分)
解方程组
,y=x-2 y=x2-
x-1 2 3 2
得
,x1= 1 2 y1=- 3 2
;x2=1 y2=-1
∴直线y=x-2与抛物线y=x2-
x-1 2
的交点为A(3 2
,-1 2
)3 2
;,&B(1,-1)
∴点A关于对称轴x=
的对称点是A′(0,-1 4
),3 2
点B关于x轴的对称点是B'(1,1),设过点A'、B'的直线解析式为y=kx+b;
∴
,b=- 3 2 k+b=1
,k= 5 2 b=- 3 2
∴直线A'B'的解析式为y=
x-5 2
;3 2
∴直线A'B'与x轴的交点为F(
,0)(5分)3 5
与直线x=
的交点为E(1 4
,-1 4
)(6分)7 8
则点E(
,-1 4
)、F(7 8
,0)为所求;3 5
过点B'做B'H⊥AA'的延长线于点H,
∴B′H=
,HA'=1;5 2
在Rt△A'B'H中,A′B′=
=B′H2+A′H2
,29 2
∴所求最短总路径的长为AE+EF+FB=A'B'=
.(7分)29 2