∵y=ax²+bx+c的图象与x轴交于点B（x₁，0），C（x₂，0），

∴x₁+x₂=-

b

a

，x₁x₂=

c

a

；

又∵x₁²+x₂²=13，即（x₁+x₂）²-2x₁x₂=13，

∴（-

b

a

）²-2•

c

a

=13，①

4a+2b+c=4，②

-

b

2a

=

1

2

．③

解由①、②、③组成的方程组，

得a=-1，b=1，c=6；

∴y=-x²+x+6；（2分）

与x轴交点坐标为（-2，0），（3，0），（3分）

与y轴交点D坐标为（0，6）；（4分）

设y轴上存在点P，使得△POB∽△DOC，则

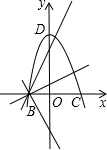（1）当B（-2，0），C（3，0），D（0，6）时，

有

OB

OC

=

OP

OD

，OB=2，OC=3，OD=6；

∴OP=4；即点P坐标为（0，4）或（0，-4）；

当P坐标为（0，4）时，可设过P、B两点直线的解析式为y=kx+4，

有0=2k+4，得k=2；

∴y=2x+4；（4.5分）

当P点坐标为（0，-4）时，可设过P、B两点直线的解析式为y=kx-4；

有0=-2k-4，

得k=-2；

∴y=-2x-4（5分）

或

OB

OD

=

OP

OC

，OB=2，OD=6，OC=3

∴OP=1，这时P点坐标为（0，1）或（0，-1）；

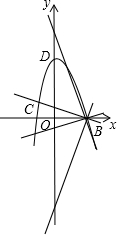当P点坐标为（0，1）时，可设过P、B两点直线的解析式为y=kx+1；

有0=-2k+1，

得k=

1

2

．

∴y=

1

2

x+1（5.5分）

当P点坐标为（0，-1）时，可设过P、B两点直线的解析式为y=kx-1；

有0=-2k-1，

得k=-

1

2

；（6分）

∴y=-

1

2

x-1；

（2）当B（3，0），C（-2，0），D（0，6）时，同理可得

y=-3x+9（6.5分）

或y=3x-9（7分）

或y=-

1

3

x+1（7.5）

或y=

1

3

x-1．（8分）