已知二次函数y=x2-2(k+1)x+4k的图象与x轴分别交于点A(x1,0)、B(x2,0),且-
(1)求k的取值范围; (2)设二次函数y=x2-2(k+1)x+4k的图象与y轴交于点M,若OM=OB,求二次函数的表达式; (3)在(2)的条件下,若点N是x轴上的一点,以N、A、M为顶点作平行四边形,该平行四边形的第四个顶点F在二次函数y=x2-2(k+1)x+4k的图象上,请直接写出满足上述条件的平行四边形的面积. |
(1)令y=0,则x2-2(k+1)x+4k=0,即(x-2k)(x-2)=0,
解方程得:x=2k或x=2,则A(2k,0),B(2,0).
由题意得,-
<2k<-3 2
,1 2
故可得:-
<k<-3 4
.1 4
(2)∵OM=OB,B的坐标为:(2,0),
∴M点坐标为:(0,-2),
把点M的坐标分别代入y=x2-2(k+1)x+4k中,可得:4k=-2,
解得:k=-
,1 2 
故二次函数表达式为:y=x2-x-2.
(3)由(2)知k=-
,则A(-1,0).1 2
①如图1,当AM为边时,AN=MF,且AN∥MF.
由(2)知,二次函数表达式为:y=x2-x-2.
∵M点坐标为:(0,-2),
∴当y=-2时,-2=x2-x-2,解得x=1或x=0,
∴点F的坐标为(1,-2)或(0,-2)(与点M重合,舍去),
∴AN=MF=1,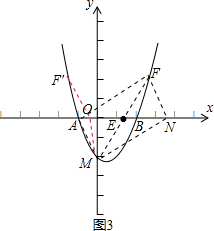
此时S▱AMFN=AN•NM=1×2=2;
②如图2,当AM为对角线时,同理证得AN=MF=1,
此时S▱AMFN=AN•NM=1×2=2;
③如图3,当AM为边时,AE=EN,ME=FE.
设F(a,b),N(t,0),
则
,
=a 2 t-1 2
=0b-2 2 b=a2-a-2
解得,
或a= 1+ 17 2 b=2 t= 3+ 17 2
,a= 1- 17 2 b=2 t= 3- 17 2
此时,S▱AMFN=AN•OM=(t+1)×2=2×
+2=5+3+ 17 2
,或S▱AMFN=AN•OM=(t+1)×2=2×17
+2=5-3- 17 2
;17
综上所述,符合条件的平行四边形的面积是:2,5+
或5-17
.17

