问题
解答题
设a为正实数，函数f（x）=x3－ax2－a2x+1, x∈R．
（1）求f（x）的极值；
（2）设曲线y=f（x）与直线y=0至多有两个公共点，求实数a的取值范围．
答案
（1）f（x）（极大）=f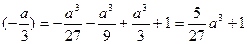
f（x）（极小）=f（a）=a3－a3－a3+1=1－a3
（2）见解析（3）0<a≤1
（1）f′（x）=3x2－2ax－a2……………………………………………………2分
由f′（x）=3x2－2ax－a2=0，得x1=－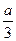
，x2="a," （a>0）
| x | 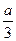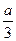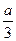（－，－） | － | （－,a） | a | （a,+ ∞） |
| f′（x） | + | 0 | － | 0 | + |
| f（x） | 增 | 极大 | 减 | 极小 | 增 |
∴f（x）（极大）=f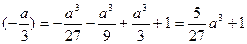
f（x）（极小）=f（a）=a3－a3－a3+1=1－a3……………………………………………7分
（2）∵f（x）在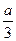（－∞，－）上递增，在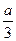（－,a）上递减，在（a,+ ∞）上递增，
f（x）（极大）=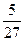
a3+1>0………………………………………………………………9分
①当极小值f（a）=1－a3≥0，即0<a≤1时，y=f（x）与y=0在x∈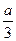（－，+∞）上有1个或0个公共点，此时f（－1）=a（a－1） ≤0
∴y=f（x）与y="0 " 在x∈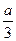（－∞，－）上有1个公共点
∴0<a≤1时，y=f（x）与y=0有1个或2个公共点……………………………11分
②当极小值f（a）=1－a3<0即a>1时，y=f（x）与y=0在x∈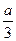（－，+∞）上有2个公共点，此时f（－a）=1－a3<0
∴y=f（x）与y="0" 在x∈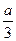（－∞，－）上有1个公共点
∴a>1时，y=f（x）与y=0有3个公共点………………………………………13分
综上，0<a≤1……………………………………………………………………14分