问题
解答题
已知:抛物线y=-x2+(2m+2)x-(m2+4m-3)
(1)抛物线与x轴有两个交点,求m的取值范围;
(2)当m为不小于零的整数,且抛物线与x轴的两个交点是整数点时,求此抛物线的解析式;
(3)若设(2)中的抛物线的顶点为A,与x轴的两个交点中右侧的交点为B,M为y轴上一点,且MA=MB,求M的坐标.
答案
(1)∵抛物线与x轴有两个交点,
∴△=b2-4ac>0
即:(2m+2)2-4×(-1)×[-(m2+4m-3)]>0
解得,m<2(2分)
(2)∵m为不小于零的整数,
∴m=0或m=1(3分)
当m=0时,y=-x2+2x+3与x轴的交点是(-1,0),(3,0);(4分)
当m=1时,y=-x2+4x-2与x轴的交点不是整数点,舍去;(5分)
综上所述这个二次函数的解析式是y=-x2+2x+3;
(3)设M(0,y),连接MA,MB,
过点A作AC⊥y轴,垂足为C;
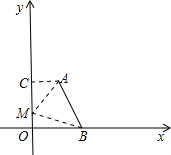
∵MA=MB
∴AC2+CM2=OM2+OB2
即:1+(4-y)2=y2+32(6分)
解得,y=1(7分)
∴M(0,1).(8分)
