已知抛物线y=-x2+2mx-m2-m+3（1）证明抛物线顶点一定在直线y=-x

问题解答题

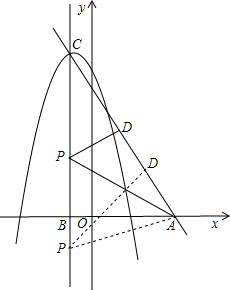
已知抛物线y=-x²+2mx-m²-m+3
（1）证明抛物线顶点一定在直线y=-x+3上；
（2）若抛物线与x轴交于M、N两点，当OM•ON=3，且OM≠ON时，求抛物线的解析式；
（3）若（2）中所求抛物线顶点为C，与y轴交点在原点上方，抛物线的对称轴与x轴交于点B，直线y=-x+3与x轴交于点A．点P为抛物线对称轴上一动点，过点P作PD⊥AC，垂足D在线段AC上．试问：是否存在点P，使S_△PAD=

S_△ABC？若存在，求出点P的坐标；若不存在，请说明理由．

答案

（1）y=-x²+2mx-m²-m+3=-（x-m）²-m+3，

∴顶点坐标为（m，-m+3），

∴顶点在直线y=-x+3上．

（2）∵抛物线与x轴交于M、N两点，

∴△＞0，

即：（2m）²-4（m²+m-3）＞0，

解得：m＜3，

∵OM•ON=3，

∴m²+m-3=±3，

当m²+m-3=-3时，m²+m=0，

∴m=0，m=-1，

∴当m=0时，y₁=-x²+3（与OM≠ON矛盾，舍），

∴m=-1，y₁=-x²-2x+3，

当m²+m-3=3时，m²+m-6=0，

∴m=2，m=-3，

∴y₂=-x²+4x-3，y₃=-x²-6x-3．

（3）∵抛物线与y轴交点在原点的上方

∴y=-x²-2x+3，

∴C（-1，4），B（-1，0），

∵直线y=-x+3与x轴交于点A，

∴A（3，0），

∵BA=BC，

∴∠PCD=45°，

∴设PD=DC=x，

则PC=

x，AD=4

-x，

∵S_△PAD=

S_△ABC，

∴

（4

-x）•x=

×4×4，x²-4

x+4=0；

解得：x=2

±2；

当x=2

+2时，PC=

x=4+2

，

∴4-y_P=4+2

，

∴y_P=-2

，

∴P（-1，-2

），

当x=2

-2时，PC=4-2

，

∴y_P=2

，

∴P（-1，2

），

∴P（-1，2

）或P（-1，-2

）．