已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.
(1)求a的值;
(2)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值;
(1)a="1" (2)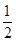
题目分析:(1)首先确定函数的定义域,然后求导,利用导数,确定函数的单调区间和极小值,此处,极小值就是最小值,由于最小值为0,可建立关于a的方程,解之即可.(2)通过x=1验证k≤0不满足条件,所以k>0,构造函数g(x)=f(x)-kx2,则g′(x)=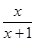 -2kx=
-2kx=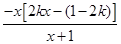 .分类讨论:k≥
.分类讨论:k≥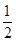 时,g′(x)<0在(0,+∞)上恒成立,总有g(x)≤g(0)=0,故k≥
时,g′(x)<0在(0,+∞)上恒成立,总有g(x)≤g(0)=0,故k≥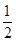 符合题意; 0<k<
符合题意; 0<k<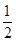 时,g(x)在
时,g(x)在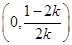 内单调递增,x0∈
内单调递增,x0∈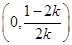 时,g(x0)>g(0)=0,故0<k<
时,g(x0)>g(0)=0,故0<k<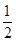 不合题意.所以k的最小值为
不合题意.所以k的最小值为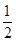 .
.
试题解析:.解:(1)f(x)的定义域为(-a,+∞).
f′(x)=1-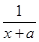 =
=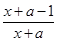 .2分
.2分
由f′(x)=0,得x=1-a>-a.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-a,1-a) | 1-a | (1-a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | | 极小值 | |
故由题意f(1-a)=1-a=0,所以a=1. 5分
(2)当k≤0时,取x=1,有f(1)=1-ln2>0,
故k≤0不合题意. 6分
当k>0时,令g(x)=f(x)-kx2,
即g(x)=x-ln(x+1)-kx2.
g′(x)=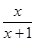 -2kx=
-2kx=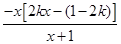 .
.
令g′(x)=0,得x1=0,x2=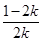 >-1. 8分
>-1. 8分
①当k≥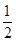 时,
时,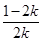 ≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,即f(x)≤kx2在[0,+∞)上恒成立,故k≥
≤0,g′(x)<0在(0,+∞)上恒成立,因此g(x)在[0,+∞)上单调递减,从而对任意的x∈[0,+∞),总有g(x)≤g(0)=0,即f(x)≤kx2在[0,+∞)上恒成立,故k≥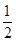 符合题意. 10分
符合题意. 10分
②当0<k<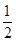 时,
时,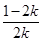 >0, 对于x∈
>0, 对于x∈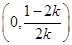 ,g′(x)>0,故g(x)在
,g′(x)>0,故g(x)在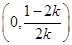 内单调递增,因此当取x0∈
内单调递增,因此当取x0∈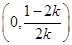 时,g(x0)>g(0)=0,即f(x0)≤kx02不成立,故0<k<
时,g(x0)>g(0)=0,即f(x0)≤kx02不成立,故0<k<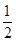 不合题意.
不合题意.
综上,k的最小值为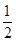 . 12分
. 12分
