问题
解答题
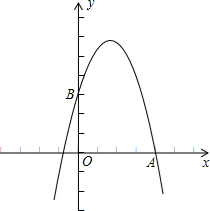
已知二次函数y=ax2+bx+3的图象经过(1,
(1)求此二次函数的解析式并画出这个二次函数的图象; (2)求线段AB的中垂线的函数解析式. |
答案
(1)∵二次函数y=ax2+bx+3的图象经过(1,
),(2,21 4
)两点,11 2
∴将两点坐标代入二次函数解析式,
得:
,a+b+3= 21 4 4a+2b+3= 11 2
解得:
,a=-1 b= 13 4
∴此二次函数的解析式为y=-x2+
x+3.13 4
图象如右所示:
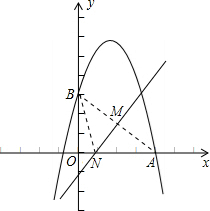 (2)解方程-x2+
(2)解方程-x2+
x+3=0,13 4
即4x2-13x-12=0,
解得x1=4,x2=-
.3 4
∵抛物线y=-x2+
x+3与x轴的两个交点的右边一个交点为点A,与y轴交于点B,13 4
∴A点坐标为(4,0),B点坐标为(0,3).
连接AB,作线段AB的中垂线MN,交AB于M,交OA于N,连接BN,则点M为AB的中点,其坐标为(2,
).3 2
设N点坐标为(x,0),则ON=x,AN=BN=4-x,
在△OBN中,∵∠BON=90°,OB=3,ON=x,BN=4-x,
∴OB2+ON2=BN2,即32+x2=(4-x)2,
解得x=
,7 8
∴N点坐标为(
,0).7 8
设直线MN的解析式为y=mx+n,
将M(2,
),N(3 2
,0)代入,7 8
得
,2m+n= 3 2
m+n=07 8
解得
,m= 4 3 n=- 7 6
∴直线MN的解析式为y=
x-4 3
.7 6
即线段AB的中垂线的函数解析式为y=
x-4 3
.7 6